
Genichi Taguchi's impact upon North American product design and manufacturing processes began in November 1981. Ford Motor Company requested that Dr. Taguchi make a presentation. Fortunately, I was invited to hear about this powerful design technique. A different method of measuring quality is central to Taguchi's approach to design. Loss function measures quality. The loss function establishes a financial measure of the user dissatisfaction with a product's performance as it deviates from a target value. Thus, both average performance and variation are critical measures of quality. Selecting a product design or a manufacturing process that is insensitive to uncontrolled sources of variation improves quality. Dr. Taguchi calls these uncontrolled sources of variation noise factors. This term comes from early applications of his methods in the communications industry. Applying Taguchi's concept entails evaluating both the variance and the average for the technical bench marking in QFD. The loss function provides a single metric for comparison.
Static Taguchi applications search for a product design or manufacturing process that attains one fixed performance level. A static application for an injection molding machine finds the best operating conditions for a single mold design. Dynamic applications use mold dimensions as the signal and search for operating conditions which yield the same percentage shrinkage for any dimension in any orientation. The dynamic approach allows an organization to produce a design that satisfies today's requirements but can be easily changed to satisfy tomorrow's demands. You can consider this latter approach as contingency planning for some unknown future requirement. In dynamic applications, a signal factor moves the performance to some value and an adjustment factor modifies the design's sensitivity to this factor. If you plot a straight line relationship, with the horizontal axis as the signal factor and the vertical axis as the response, the adjustment factor changes the slope of the line. Being able to reduce a product's sensitivity to changes in the signal is useful. For example, if you are designing a sports car your desired outcome might be a car that allows the driver to change the feel of the road. The signal factor would be a control knob setting. The analysis could determine that the suspension system is the adjustment factor. The adjustment factor adjusts the magnitude of change in road feel to a given change in the knob setting. Several other design specifications would assure a predictable relationship in the control knob setting and the feel. Changes in road conditions and weather would have minimal effect upon the relationship between knob adjustment and feel of the road.
Listening to the voice of the customer helps organizations create good systems designs. Some teams use focus groups to gather input for these designs. Fortune Magazine (April 1995) has an article by Justin Martin entitled "Ignore Your Customer." It presents several examples of products that were strongly influenced by the voice of focus groups, but they were not purchased by consumers. The author suggests that studying the customers under natural conditions would provide additional useful information. Going to the Gemba is a crucial step in QFD. This has been advocated since 1985. The Gemba is the total environment in which the customer lives and works.
Voice of the Customer Table with three components: customer verbatim response, context of use and integration of verbatim response and context (Chapter 4, Figure 4-5). Eventually, the team divides this expanded list of customer information into demanded qualities, failure modes, solutions, etc. The Context of Application Table (Figure 4-3) identifies some of the environmental sources of uncontrolled variation in product performance. Some examples of sources of variation for an easel pad are the force applied to the paper, humidity, and whether is it being used inside or outside. Taguchi's Robust Design reduces the impact of uncontrolled sources of variation upon the product's performance.
How to Measure Quality
Traditionally, quality is viewed as a step function as shown by the heavy line graph in the figure 1. A product is either good or bad. This view assumes a product is uniformly good between the specifications (LS the lower specification and US the upper specification). The vertical axis represents the degree of displeasure the customer has with the product's performance. Curves A and B represent the frequencies of performance of two designs during a certain time period. B has a higher fraction of "bad" performance and therefore is less desirable than A.

figure 1
Sometimes traditional decision makers and those using Taguchi's loss function will make the same judgments. If organizations consider both the position of the average and the variance, and if the averages are equal and/or the variances are equal, then the traditional decision maker and one using Taguchi's loss function will make the same decision. However, the traditional decision-maker calculates the percent defective over time when both the average and variance are different.

figure 2
Taguchi believes that the customer becomes increasingly dissatisfied as performance departs farther away from the target.
He suggests a quadratic curve to represent a customer's dissatisfaction with a product's performance. The quadratic curve is the first term when the first derivative of a Taylor Series expansion about the target is set equal to zero. The curve is centered on the target value, which provides the best performance in the eyes of the customer. Identifying the best value is not an easy task. Targets are sometimes the designer's best guess.
LCT represents lower consumer tolerance and UCT represents upper consumer tolerance. This is a customer- driven design rather than an engineers specification. Experts often define the consumer tolerance as the performance level where 50% of the consumers are dissatisfied. Your organization's particular circumstance will shape how you define consumer tolerance for a product.
The equation for the target-is-best loss function uses both the average and the variance for selecting the best design. The equation for average loss is:
|
|
Calculating the average loss permits a design team to consider the cost benefit analysis of alternate designs with different costs yielding different average losses. As seen in figure 2, there is some financial loss incurred at the upper consumer tolerance. This could be a warranty charge to the organization or a repair expense.
Most applications of the loss function in QFD can use a value of 1 for k since the constant would be the same for all competitors as it relates to the customer.
The graphics show a symmetric loss about the target, but this is not always the case.
If two products have the same variance but different averages, then the product with the average that is closer to the target (A) has better quality figure 3.
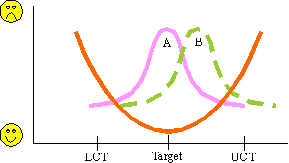
figure 3
If two products have the same average but different variance, then the product with the smaller variance has better quality figure 4. Product B performs near target less often than its competitor.
figure 4
What if both average and variance are different? Calculating the average loss assumes you agree with the concept of the loss function. The product with smaller loss has the better quality figure 5. If curve A is far to the right, then curve B would be the better. If curve A is centered on the target, then curve A would be better. Somewhere in between, both have the same loss.

figure 5
Loss Function and Technical Bench Marking
Teams should gather data collected for technical bench marking in a real environment. A real environment is one in which everything is not controlled and ideal. Our product and the competitor's product would be evaluated at different temperatures, humidity and other conditions. The laboratory can simulate these conditions. By evaluating the product's performance in several environmental conditions, you would have realistic data to calculate the real world variance.
|
An orthogonal array can define a balanced study of different environmental conditions. The two or three important environmental conditions, each at two levels, provide a good estimate of the environmental variation. The humidity is represented by H, the weight of items taped to the sheet on the wall by W, and the surface texture by T. The 1 and 2 under H represent high and low humidity. The four different combinations of environments are used to determine the average and variance of each product's performance. |
|
|
|
Instead of using all eight different combinations, the orthogonal array uses a special subset of the eight. Due to the balanced nature of these four combinations, the effect of the missing four can be predicted. |
Another option is to select the best and the worst environmental combination of the eight combinations. This approach further reduces the number of environments evaluated to two.
The average loss for the data is:
|
|
The calculations of the variance and loss can be entered in two additional rows at the bottom of the Demanded Quality vs. Performance matrix used in QFD. The ratio of the average loss of one competitor to another is independent of k. The information of the average, variance and loss ratio identifies the directions for improvement as defined by the average loss equation.